Stable Diffusion 神经网络深度知识图谱

1. VAE (Variational Autoencoder)

图像压缩机 | 潜空间映射

Status: Frozen ❄️

关键技术原理

●
感知压缩 (Perceptual Compression): 将像素空间 ($H \times W \times 3$) 压缩至潜空间 ($\frac{H}{8} \times \frac{W}{8} \times 4$)。压缩因子 $f=8$，计算量减少 64 倍。
●
变分分布预测: 编码器不直接输出结果，而是预测高斯分布的参数：均值 ($\mu$) 和 对数方差 ($\log\sigma^2$)。
●
KL 散度损失: 训练时迫使潜空间分布接近标准正态分布 $\mathcal{N}(0, 1)$，保证生成的多样性和平滑性。

🧮 Nano VAE 计算实例

1. 输入图像 (2x2 Patch)

X = \begin{bmatrix} 100 & 120 \\ 80 & 100 \end{bmatrix}

微型图像块示例，用于演示 VAE 压缩。

2. 编码器预测分布参数

假设神经网络计算得出：
$\mu = 2.5$, $\log\sigma^2 = -0.5$

3. 重参数技巧 (Reparameterization Trick)

公式: $z = \mu + \exp(0.5 \times \log\sigma^2) \cdot \epsilon$

随机抽取噪声 $\epsilon = 0.5$ (不可训练):

\sigma = \exp(-0.25) \approx 0.779 $$ $$ z = 2.5 + (0.779 \times 0.5) = \mathbf{2.8895}

重参数技巧将不可导的采样过程转化为可训练流程。

结果：4 个像素被压缩为 1 个潜变量数值。

2. CLIP (Text Encoder)

跨模态翻译官 | 语义理解

Status: Frozen ❄️

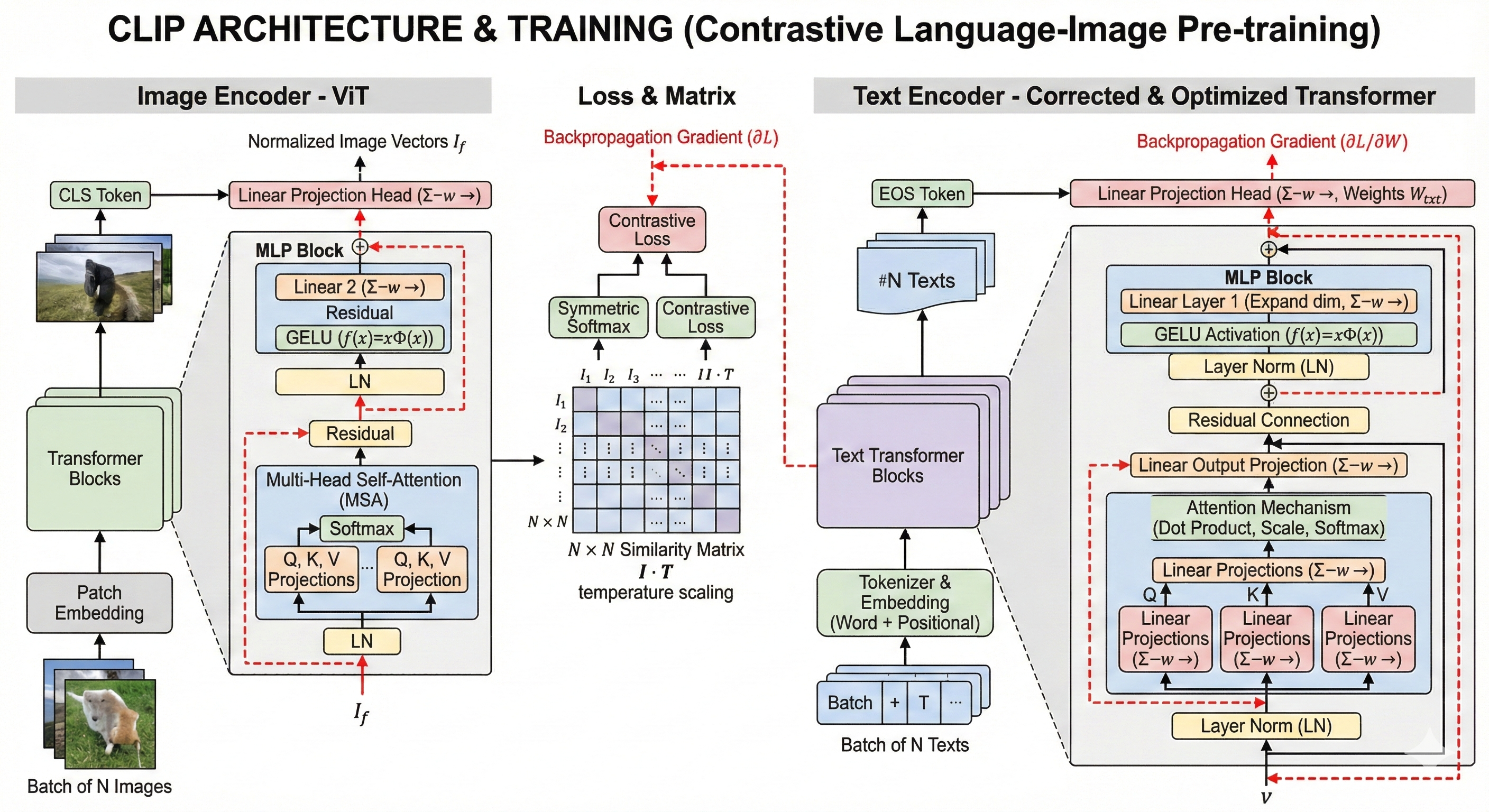
关键技术原理

●
掩码自注意力 (Masked Self-Attention): 采用类似 GPT 的单向注意力机制。每个 token 只能看到它左边的词。这迫使信息像滚雪球一样向后传递。
●
EOS Token 聚合: 由于掩码机制，全句的完整语义最终汇聚在最后一个标记 [EOS] (End of Sequence) 上。SD 使用该向量作为全局条件 $c$。
●
对比损失 (Contrastive Loss): 训练目标是最大化匹配图文对的余弦相似度，最小化不匹配对的相似度。

🧮 Nano CLIP 计算实例

Prompt: "Red Cat"

Step 1: Embedding (查表)

"Red" -> [1.0, 0.0] (红色特征)

"Cat" -> [0.0, 1.0] (猫特征)

Step 2: Attention 聚合 (在 EOS 处)

假设 EOS token 注意力权重平分：

c = 0.5 \times [1, 0] + 0.5 \times [0, 1] = [0.5, 0.5]

CLIP 文本注意力在 EOS 处对颜色与物体语义进行等权融合。

这个向量 [0.5, 0.5] 融合了“既红又猫”的语义，作为 Key 和 Value 进入 U-Net。

3. Scheduler (调度器)

噪声指挥官 | 时间步控制

Status: Math (No Weights)

关键技术原理

前向加噪 (Forward Process): 利用 $\bar{\alpha}_t$ (累乘保留率) 实现“一步到位”计算：
$z_t = \sqrt{\bar{\alpha}_t} z_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon$
扩散调度器在任意时间步的闭式加噪公式。
Cosine Schedule (余弦调度): 相比线性调度，余弦曲线让 $\bar{\alpha}_t$ 下降得更平滑，避免图像在训练早期就变成纯噪声，提高训练效率。

参数关系图谱

$\beta_t$: 单步加噪量 (很小)

$\alpha_t = 1 - \beta_t$: 单步保留量

$\bar{\alpha}_t = \prod \alpha_i$: 累积保留量 (随 $t$ 增大趋近 0)

训练时: 随机采样 $t$，直接计算 $z_t$。

推理时: 逐步去噪 $z_t \to z_{t-1}$。

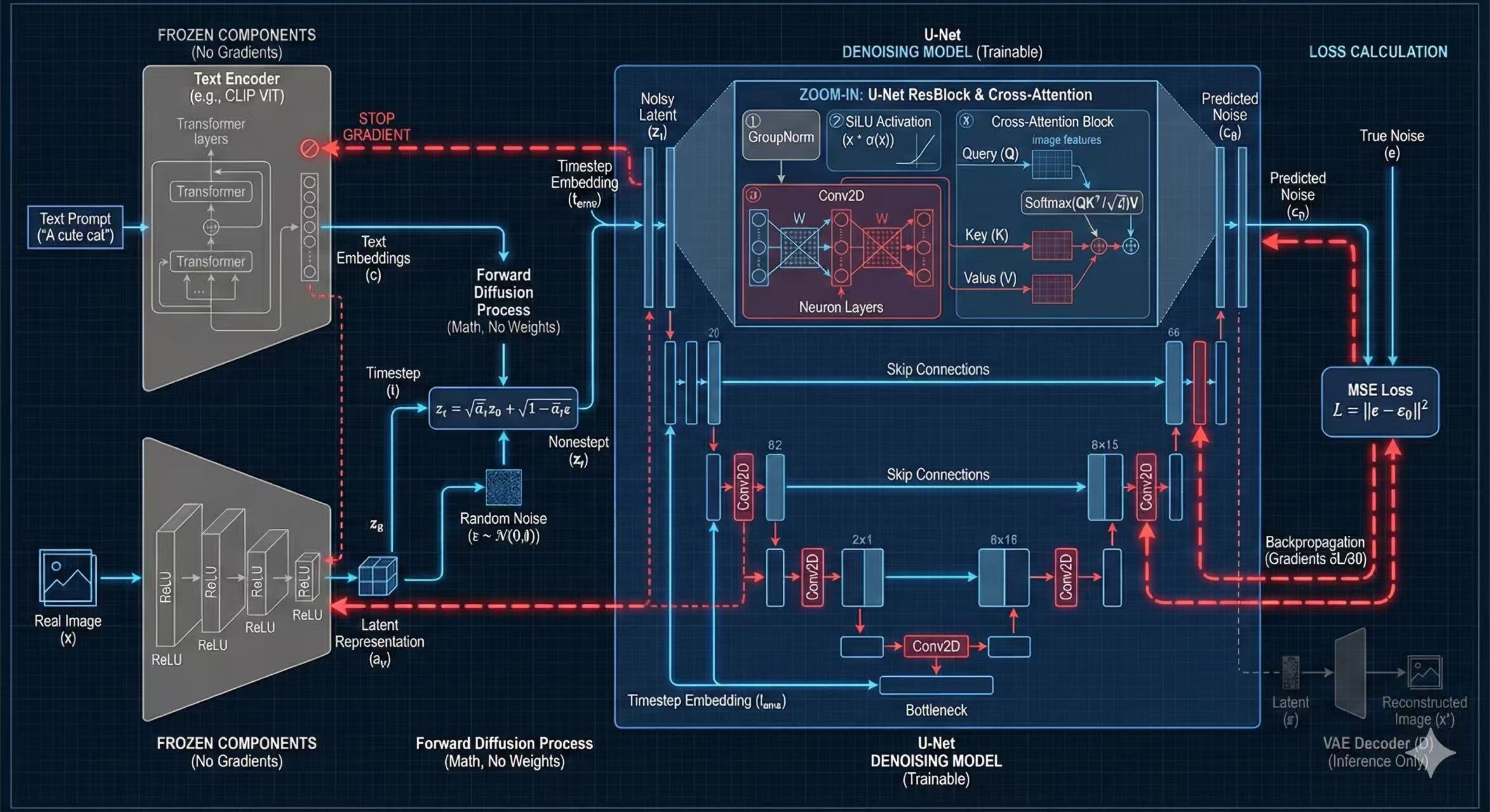
4. U-Net (Denoising Model)

核心去噪画师 | 训练与预测的主角

Status: Trainable 🔥

🔧 内部架构拆解

ResBlock (残差块)

负责处理图像的空间特征（Conv2D）。解决“画在哪里”的问题。在第一层（高分辨率）起主导作用。

Cross-Attention (交叉注意力)

负责注入文本信息。$Q$(图) 查 $K$(文)。公式：
$Softmax(\frac{QK^T}{\sqrt{d}})V$

Skip Connection (跳跃连接)

将左侧编码器的特征直接复制到右侧解码器。在第一层，它传递的是原始图像特征（因为无 Attention）。

A

U-Net 训练全过程演算 (Nano U-Net)

Step 0: 场景设定

输入图像 X (4x4, 原图+噪声):

X = \begin{bmatrix} 1 & 1 & 2 & 2 \\ 1 & 1 & 2 & 2 \\ 3 & 3 & 4 & 4 \\ 3 & 3 & 4 & 4 \end{bmatrix}

示例噪声图像，在 U-Net 编码端作为高分辨率特征输入。

文本向量 c (Red Cat):

"Red": [10, 0]

"Cat": [0, 10]

1

左侧 Layer 1 (编码)

通常第一层无 Attention，只做卷积。假设卷积为恒等映射。

输出 $F_1$: 等于输入 $X$。

关键动作：存档 Skip Connection $F_{skip\_L1} = X$

(这是原始的 1,2,3,4 结构，没有被文本污染)

2

瓶颈层 (Bottleneck) & Attention

下采样到 1x1 像素，进行深层图文融合。

1. 下采样特征: [9] (假设值)

2. 生成 Q: [9, 9]

3. 计算 Score ($Q \cdot K^T$): 对 Red 90, 对 Cat 90。

4. Softmax: [0.5, 0.5] (平分秋色)

5. 加权求和: $0.5 \times [10,0] + 0.5 \times [0,10] = [5, 5]$

6. 最终输出: 10 (投影求和)

3

右侧 Layer 1 (解码 & 融合)

上采样并融合跳跃连接。这是恢复细节的关键。

1. 上采样: 将瓶颈层的 10 放大为 4x4 矩阵 (全 10)。

F_{up} = \text{All } 10

上采样将语义向量广播回空间网格。

2. 融合 (Fusion): $F_{up} + F_{skip\_L1}$

\epsilon_\theta = \begin{bmatrix} 10 & 10 & 10 & 10 \\ \dots & \dots & \dots & \dots \end{bmatrix} + \begin{bmatrix} 1 & 1 & 2 & 2 \\ \dots & \dots & \dots & \dots \end{bmatrix} = \begin{bmatrix} 11 & 11 & 12 & 12 \\ 11 & 11 & 12 & 12 \\ 13 & 13 & 14 & 14 \\ 13 & 13 & 14 & 14 \end{bmatrix}

跳跃连接与解码端特征相加，恢复空间细节。

成功保留了左上角(11)和右下角(14)的空间结构差异！

4

损失计算 (MSE Loss)

对比预测噪声与真噪声。

假设真噪声 $\epsilon$ 左上角为 1.5。

预测噪声 $\epsilon_\theta$ 左上角为 11。

Loss: $(1.5 - 11)^2 = (-9.5)^2 = \mathbf{90.25}$

→ 反向传播梯度，修正 U-Net 权重。

5. 推理/采样 (Inference)

从噪声到图像 | DDPM 算法

Algorithm: DDPM

核心公式解析

x_{t-1} = \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta(x_t, t) \right) + \sigma_t z

DDPM 去噪更新方程，左项为确定性校正，右项为随机多样性。

缩放系数 防止数值方差爆炸

去噪项 (核心) 减去 U-Net 预测的噪声

随机项 ($+ \sigma_t z$) 增加多样性 (创造力)

B 推理演算实例 (Step $t=3 \to t=2$)

1. 当前状态: $x_3 = 1.5$ (纯随机噪声)

2. U-Net 预测: $\epsilon_\theta = 0.5$

3. 确定性去噪:

假设去噪系数计算为 0.426

\text{中间值} = 1.5 - (0.426 \times 0.5) = 1.287 $$ $$ \text{缩放后} \approx 1.538

确定性项将噪声向真实信号拉近。

4. 注入随机性 (Creativity):

加入随机噪声 $z=0.8$, 系数 $\sigma=0.55$

x_2 = 1.538 + (0.55 \times 0.8) = \mathbf{1.976}

随机项保证采样多样性，避免模式崩塌。

结果：图像从 1.5 (纯噪) 变为 1.976 (更接近有效信号)。